Question

In the book Advanced Managerial Accounting, Robert P. Magee discusses monitoring cost variances. A cost variance is the difference between a budgeted cost and an actual cost. Magee describes the following situation:

Michael Bitner has responsibility for control of two manufacturing processes. Every week he receives a cost variance report for each of the two processes, broken down by labor costs, materials costs, and so on. One of the two processes, which we'll call process A , involves a stable, easily controlled production process with a little fluctuation in variances. Process B involves more random events: the equipment is more sensitive and prone to breakdown, the raw material prices fluctuate more, and so on.

"It seems like I'm spending more of my time with process B than with process A," says Michael Bitner. "Yet I know that the probability of an inefficiency developing and the expected costs of inefficiencies are the same for the two processes. It's just the magnitude of random fluctuations that differs between the two, as you can see in the information below."

"At present, I investigate variances if they exceed $2,659, regardless of whether it was process A or B. I suspect that such a policy is not the most efficient. I should probably set a higher limit for process B."

The means and standard deviations of the cost variances of processes A and B, when these processes are in control, are as follows: (Round your z value to 2 decimal places and final answers to 4 decimal places.):

Process A Process B
Mean cost variance (in control) $ 3 $ 1
Standard deviation of cost variance (in control) $5,473 $9,743
Furthermore, the means and standard deviations of the cost variances of processes A and B, when these processes are out of control, are as follows:
Process A Process B
Mean cost variance (out of control) $7,651 $ 6,169
Standard deviation of cost variance (out of control) $5,473 $9,743


(a)
Recall that the current policy is to investigate a cost variance if it exceeds $2,659 for either process. Assume that cost variances are normally distributed and that both Process A and Process B cost variances are in control. Find the probability that a cost variance for Process A will be investigated. Find the probability that a cost variance for Process B will be investigated. Which in-control process will be investigated more often?

Process A
Process B
(Click to select)Process AProcess B is investigated more often.
(b)
Assume that cost variances are normally distributed and that both Process A and Process B cost variances are out of control. Find the probability that a cost variance for Process A will be investigated. Find the probability that a cost variance for Process B will be investigated. Which out-of-control process will be investigated more often?

Process A
Process B
(Click to select)Process AProcess B is investigated more often.
(c) If both Processes A and B are almost always in control, which process will be investigated more often?
(Click to select)Process BProcess A will be investigated more often.
(d)
Suppose that we wish to reduce the probability that Process B will be investigated (when it is in control) to .3121. What cost variance investigation policy should be used? That is, how large a cost variance should trigger an investigation? Using this new policy, what is the probability that an out-of-control cost variance for Process B will be investigated?

k= __________
P(x > 4,775)= ________

Answer 1

a.

P(A > 2,659)= 0.5239

P(B > 2,659)= 0.4325

Process A will be investigated more often.

b.

P(A > 2,659) = 0.8186

P(B > 2,659)= 0.6406

Process A will be investigated more often.

d.

K= 5.7741

P(B> 5.77409)= 0.51595

Explanation:

Hello!

The cost variance is defined as the difference between a budget cost and an actual cost.

There are two processes of interest:

Process A: stable: easily controlled production process with little fluctuation invariance.

Process B: random events: the equipment is more sensitive and prone to breakdown, the raw material prices fluctuate more,...

Since he's paying more attention to B, even though both processes have the same probability of developing inefficiency, he decides to investigate each process if their variances exceed $2659 regardless of what the process is.

In control:

Process A

Mean cost variance (in control) $ 3

The standard deviation of cost variance (in control) $5,473

Process B

Mean cost variance (in control) $ 1

The standard deviation of cost variance (in control) $9,743

Out of control

Process A

Mean cost variance (out of control) $7,651

The standard deviation of cost variance (out of control) $5,473

Process B

Mean cost variance (out of control) $ 6,169

The standard deviation of cost variance (out of control) $9,743

a) The cost variances of both processes have a normal distribution, they will be investigated if the cost variance is greater than $2,659, symbolically:

Both are "in control" so you have to use the given data for this characteristic.

P(A > 2,659)

And

P(B > 2,659)

Since both variables have a normal distribution you can calculate these probabilities using the standard normal distribution as:

For process A

P(A > 2,659) = P(Z>
`(2.659 - 3)/(5.473)`)

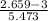P(Z>-0.06)= 1 - P(Z ≤ -0.06) = 1 - 0.47608= 0.52392

For process B

P(B > 2,659)= P(Z>
`(2.659 - 1)/(9.743)`)

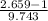P(Z> 0.17)= 1 - P(Z ≤ 0.17)= 1 - 0.56749= 0.43251

Process A will be investigated more often.

b. For this item you have to calculate the probability that the process are going to be investigated, asuming the cost variances have normal distribution, but the processes are out of control. This means you have to use the values of the second data set.

For process A

P(A > 2,659) = P(Z>
`(2.659 - 7,651 )/(5.473)`)

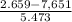P(Z>-0.91)= 1 - P(Z ≤ -0.91) = 1 - 0.18141= 0.81859

For process B

P(B > 2,659)= P(Z>
`(2.659 - 6,169 )/(9.743)`)

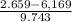P(Z> -0.36)= 1 - P(Z ≤ -0.36)= 1 - 0.35942= 0.64058

Process A will be investigated more often.

c. Looking at the probabilities of both process "out of control", process A has a grater probability than process B of having a variance cost greater than $2.659. That's why process A will be investigated more often.

d.

In this case, they want to know what is the number of cost variance that leads process B "in control" to have a probability of 0.3121 of being investigated. In this case, you have to do a reverse standardization, this means, you know the probability and need to look for its corresponding value.

P(Z>k)= 0.3121

P(Z>k) = 1 - P(Z ≤ b)

1 - P(Z ≤ k)= 0.3121

P(Z ≤ k)= 1 - 0.3121

P(Z ≤ k)= 0.6879

Now you have to look in the table for the number "b"that corresponds to the cummulative probability of 0.6879,

k= 0.49

Now k=
`(K- mu)/(sigma)`

`0.49= (K - 1)/(9.743)`

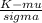
0.49*9.743= K - 1

4.77409 + 1 = K

K= 5.77409

Process B will be investigated if its cost variance is greater than $5.77409

Using this new policy you need to calculate the probability of B "out of control" to be investigated:

P(B> 5.77409) = P(Z>
`(5.77409 - 6,169 )/(9.743)`)

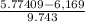P(Z> -0.04)= 1 - P(Z ≤ -0.04)= 1 - 0.48405= 0.51595

I hope it helps!