Question

asked Sep 12, 2021 129k views

1 Answer

BPX · Answer 1 · 2021-09-15T22:16:28+0000

Cylinders A and B are similar solids. The base of cylinder A has a circumference of 4π units. The base of cylinder B has an area of 9π units.

The dimensions of cylinder A are multiplied by what factor to produce the corresponding dimensions of cylinder B?

Dimensions of cylinder A are multiplied by
(3)/(2) to produce the corresponding dimensions of cylinder B

Cylinders A and B are similar solids.

The base of cylinder A has a circumference of
$4 \pi$ units

The base of cylinder B has an area of
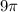$9 \pi$ units

Let "x" be the required factor

From given question,

Dimensions of cylinder A are multiplied by what factor to produce the corresponding dimensions of cylinder B

Therefore, we can say,

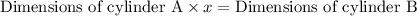
$\text{Dimensions of cylinder A} * x = \text{Dimensions of cylinder B }$

The circumference of base of cylinder (circle ) is given as:

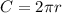
$C = 2 \pi r$

Where "r" is the radius of circle

Given that base of cylinder A has a circumference of
$4 \pi$ units

Therefore,

$4 \pi = 2 \pi r\\\\r = 2$

Thus the dimension of cylinder A is radius = 2 units

The area of base of cylinder (circle) is given as:

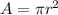
$A = \pi r^2$

Given that, the base of cylinder B has an area of
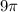$9 \pi$ units

Therefore,

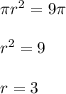
$\pi r^2 = 9 \pi\\\\r^2 = 9\\\\r = 3$

Thus the dimension of cylinder B is radius = 3 units

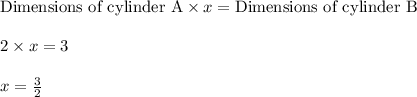
$\text{Dimensions of cylinder A} * x = \text{Dimensions of cylinder B }\\\\2 * x = 3\\\\x = (3)/(2)$

Thus dimensions of cylinder A are multiplied by
(3)/(2) to produce the corresponding dimensions of cylinder B

Please log in or register to add a comment.