Question

Can someone help me with these questions

Answer 1

Explanation:

When you take the n-th root of a number, you can rewrite the expression by taking it to the 1/n-th power. For example:

`\sqrt[n]{x} =x^(1)/(n)`

For the first expression, we can use this proprtery to get:

`\sqrt[5]{a^x} =(a^x)^(1)/(5)`

Using exponent rules, you can combine the exponents by simply multiplying them to get:

`a^(x)/(5)`

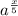
Moving on to the second expression. It is now the square root, or equivalently a 1/2 power. If we break up the terms under the radical into powers of 2, we can cancel a lot of the terms:

`(√(81a^3b^1^0) )/(√(3)a ) =(√(81a^2*a*b^1^0) )/(√(3)a )`

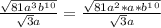
The a^2 and b^10 can be taken out of the radical because they have perfect roots:

`(√(81a^2*a*b^1^0) )/(√(3)a )=ab^5(√(81a) )/(√(3)a )`

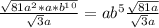
The square root of 81 has a perfect root of 9. We have:

`ab^5(√(81a) )/(√(3)a )=9ab^5(√(a) )/(√(3)a )`

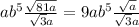
You can divide 9 and the square root of 3 by breaking up 9 into a product:

`((3*3)ab^5)/(√(3) ) (√(a) )/(a )=3√(3) ab^5(√(a) )/(a )`

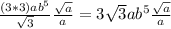
Simply by cancelling the 'a' terms to get:

`3√(3) ab^5(√(a) )/(a )={3√(3)}√(a)b^5=3b^5√(3a)`