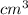Answer:
The density of water will be 0.935 g/
Step-by-step explanation:
It is sufficient to solve this as a 2D problem since the length of the dowel does not matter. Let p be the density of the dowel in g/cm^3, and take water density 1g/cm^{3}
The area of the whole circle is
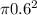 = 1.130
= 1.130
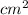
The angle from the center of the dowel to the two water line edges is
T = (2)arccos)
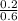
So the area exposed above water is sector minus triangle:
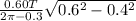
= 0.642 - 0.447
= 0.195
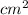
So, the weight of the dowel is balanced by the weight of water displaced:
1.130 p
= (1.130 - 0.195)
p = 0.935 g/