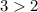Question

Please help.

Which of the following equations has a graph that is narrower than the graph of y = 2x2 + 3?


y = 2x2 − 3


y = 0.5x2 + 3


y = −3x2 + 2


y = −0.5x2 − 2

Answer 1

Answer: THIRD OPTION.

Explanation:

By definition, the graph of Quadratic function is a parabola.

The Standard form of a Quadratic function is the following:

`f(x)=ax^2+bx+c`

Where "a", "b" and "c" are real numbers (
`a\\eq 0`)

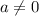It is important to remember that if the value of the leading coefficient "a" is larger, then the parabola will be narrower.

So, given the following Quadratic equation:

`y = 2x^2 + 3`

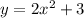
You can identify that:

`|a|=2`

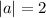
Therefore, the equation that has a graph that is narrower than the given graph, must have a leading coefficient larger than 2.

Based on this, you can conclude that that equation would be:

`y = -3x^2 + 2`

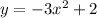
Where:

`|a|=3`

Notice that:

`3>2`