Answer:
Therefore the diagonal is 31.6 unit.
Explanation:
Given:
In a Rectangle
Length = L = 30 unit = Longer Leg
Width = W = 10 unit = Shorter Leg
Diagonal = d = Hypotenuse
To Find:
Relation between L ,W and d
d = ?
Solution:
In a Rectangle vertex angles are 90°
In Right Angle Triangle , By Pythagoras theorem we have
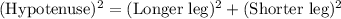
Substituting the values we get
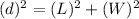
i.e
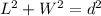 .........Relation between L ,W and d
.........Relation between L ,W and d
Now Substituting L = 30 ,W =10 we get

Therefore the diagonal is 31.6 unit.