Answer:
After the collision, they move with a speed of 13.57 m/s at 56.30° south of east
Step-by-step explanation:
Conservation Of Momentum
The total momentum of a system of particles with masses m1,m2,...mn that interact without the action of external forces, is conserved. It means that, being
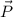 and
and
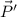 the initial and final momentums respectively:
the initial and final momentums respectively:

Or equivalently, for a two-mass system
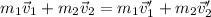
All the velocities are vectors. Let's express the velocities in magnitude v and direction
 as
as
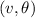 . It's rectangular components will be
. It's rectangular components will be
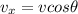
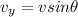
The first car is moving east at 21.2 m/s. Its velocity is
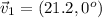
Recall that East is the zero-degree reference for angles
Expressing in rectangular form:

The second car is moving south at 17.5 m/s. Its velocity is

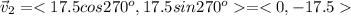
The total initial momentum is
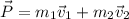
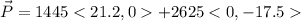
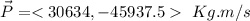
They collide and stick together in a common mass and velocity \vec v', thus
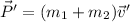
It must be equal to the initial momentum, thus
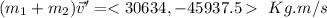
Solving for
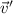
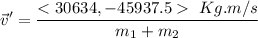
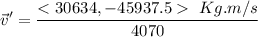
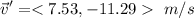
The magnitude of \vec v' is
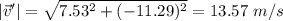
The direction angle is
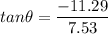
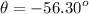
After the collision, they move with a speed of 13.57 m/s at 56.30° south of east