Answer:
⠀
Explanation:
The triangle having two sides equal along with one different side is called an isosceles triangle.
⠀
- So, Let us assume the other sides (two equal sides) of the isosceles triangle as x. As the different side is already given in the question.
⠀
We know that,
- The sum of all angles of a triangle is 180°
⠀
So, According to the question :
⠀
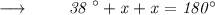
⠀
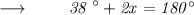
⠀
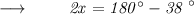
⠀

⠀
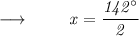
⠀
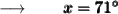
⠀
Therefore,
- The measure of the two other angles of the isosceles triangle are 71° and 71°.