Question

All three sides of a triangle are initially 5.0 long. One of the triangle's sides is oriented horizontally. The triangle is scaled in size without changing any of the angles. What is the new height of the triangle when the area is 0.7 of the original triangle's area

Answer 1

h = 3.62

Explanation:

First, as both triangles have the same angles we can use the relationship of areas and sides corresponding to similar triangles as follows:

`relation\ between\ areas=( relation\ between\ sides)^2\\(0.7A)/(A)=((s)/(5))^2\\s= 5\sqrt0.7= 4.18`

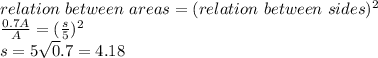
Now we know that the new triangle has sides of 4.18. Then, as these triangles are equilateral we can use the Pythagorean Theorem to find the height:

`4.18^2=h^2+((4.18)/(2))^2\\h=\sqrt (4.18^2-2.09^2)=3.62 m\\h= 3.62`

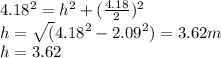
Finally the height of this new triangle is 3.62 cm