Question

A shipping clerk packs a cube with side lengths of 8 inches into a box with side lengths of 10 inches. What is the volume of the space left in the larger box

Answer 1

The volume of the space left in the larger box after packing a smaller cube inside is 488 cubic inches, calculated by subtracting the volume of the smaller cube (512 cubic inches) from the volume of the larger box (1000 cubic inches).

Step-by-step explanation:

To find the volume of the space left in the larger box, we need to calculate the volume of both the larger box and the smaller cube. The formula for finding the volume of a cube is V = s³, where s is the side length of the cube.

The volume of the larger box is V = 10 inches x 10 inches x 10 inches = 1000 cubic inches.

The volume of the smaller cube is V = 8 inches x 8 inches x 8 inches = 512 cubic inches.

To find the remaining volume in the larger box, subtract the volume of the smaller cube from the volume of the larger box:
Remaining Volume = 1000 cubic inches - 512 cubic inches = 488 cubic inches.

Therefore, the volume of the space left in the larger box after the smaller cube is packed inside it is 488 cubic inches.

Answer 2

Volume left is 488 cubic inches.

Step-by-step explanation:

Given:

Length of the small box (a) = 8 inches

Length of the big box (A) = 10 inches

The boxes are of the shape of cube.

The small cube is placed inside the big cube. We need to find the volume of the space left.

We know that, volume of a cube is equal to the cube of its side length.

Therefore, volume of small box is given as:

`V_s=a^3=(8\ in)^3=512\ in^3`

Volume of the big cube is given as:

`V_b=(A)^3=(10\ in)^3=1000\ in^3`

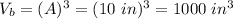
Now, volume of the space left can be calculated by subtracting the volume of the small box from the volume of the big box.

Therefore, volume of the space left is given as:

`V_(space)=V_b-V_s\\\\V_(space)=1000-512=488\ in^3`

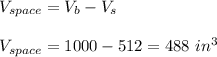
Therefore, the volume of the space left in the larger box is 488 cubic inches.