Question

Picture will be attached please help its analytic trigonometry identities.

Answer 1

14. 46.2 ft (nearest tenth)

15. 95.5° (nearest tenth)

Explanation:

Question 14

The diagonal of the square (from home plate to second base) is:

`√(65^2+65^2) =91.92388155...`

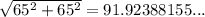
Half of this is 45.9619... ft.

Therefore, ∠ABC is not 90° and so triangle ABC is NOT a right triangle.

To determine length AB we must use the cosine rule:

`c^2=a^2+b^2-2ab \cos C`

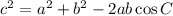
(where a and b are the sides, C is the include angle, and c is the side opposite the angle)

Given:

• a = BC = 41.5 ft
• b = AC = 65 ft
• c = AB
• C = 45°

Substituting given values into the formula:

`\implies c^2=41.5^2+65^2-2(41.5)(65) \cos (45)`

`\implies c^2=1722.25+4225-5395 \cdot (√(2) )/(2)`

`\implies c^2=2132.408915...`

`\implies c=\pm√(2132.408915...)`

`\implies c=\pm46.17801333...`

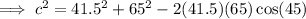
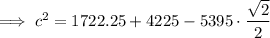
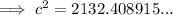
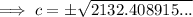
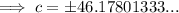
As distance is positive, c = 46.2 ft (nearest tenth)

Question 15

We need to find angle B.

Use the sine rule:

`(\sin(A))/(a)=(\sin(B))/(b)=(\sin(C))/(c)`

(where A, B and C are the angles, and a, b and c are the sides opposite the angles)

IMPORTANT: As angle B is obtuse (more than 90° and less than 180°), the sine of an obtuse angle = sine of its supplement

Therefore, sin B = sin (180 - B)

Given:

• C = 45°
• c = 46.17801333...
• b = AC = 65
• sin B = sin (180 - B)

`\implies (\sin(180-B))/(65)=(\sin(45))/(46.17801333...)`

`\implies \sin(180-B)=(65 \sin(45))/(46.17801333...)`

`\implies 180-B=84.45515638...`

`\implies B=180-84.45515638...`

`\implies B=95.54484362...`

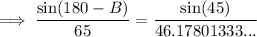
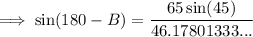
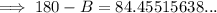
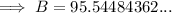
Therefore, B = 95.5° (nearest tenth)

** Note: if you use the rounded solution for c, where c = 46.2, in this calculation, then angle B will be 95.8° to the nearest tenth**