Answer:
1)$11,978
2)9%
3)15 periods
4) 6%
5) $ 78,867.70
Step-by-step explanation:
PV Annuity per period rate time
1. ? 3,000 8% 5
2. 242,980 75,000 ? 4
3. 161,214 20,000 9% ?
4. 500,000 80,518 ? 8
5. 250,000 ? 10% 4
1)

C 3,000.00
time 5
rate 0.08
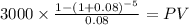
PV $11,978.1301
2)
solved using excel goal seek or financial calculator

C 75,000.00
time 4
rate 0.089998108 we set up the formula PV(A2;4,75000)
then we use goal seek to find which value of a2(which is the argument for rate) makes the formula equal to 242980
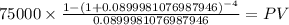
PV $242,980.0000
3)

C $20,000.00
time n
rate 0.09
PV $161,214.0000
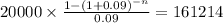
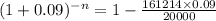
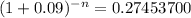
![-n= \frac{log0.274537}{log(1+0.09)]()
-15.00004401
4)
same as (2) solved using excel

C 80,518.00
time 8
rate 0.06000009
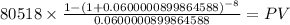
PV $500,000.0000
5)

PV 250,000
time 4
rate 0.1
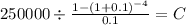
C $ 78,867.701