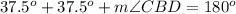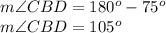Question

Given:
AB= BC
Angle BDC = 3712°
< CBD =
37.5
60
105

Answer 1

`m\angle CBD=105^o`

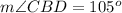
Explanation:

see the attached figure to better understand the problem

step 1

Find the measure of angle ADB

Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

In the triangle ADB

`60^o+60^o+m\angle ADB=180^o`

`m\angle ADB=180^o-120^o=60^o`

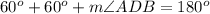
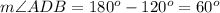
Triangle ADB is an equilateral triangle (has three equal interior angles and three equal sides)

step 2

Find the measure of the angle CBD

we know that

An isosceles triangle has two equal sides and two equal angles

In this problem triangle BDC is an isosceles triangle

Because

AB=BC ---> given problem

AB=BD ---> by equilateral triangle

BD=BC ----> by transitivity

therefore

`m\angle BDC=m\angle BCD`

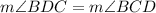
we have

`m\angle BDC=37(1)/(2)^o=37.5^o`

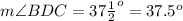
so

`m\angle BCD=37.5^o`

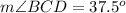
Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

In the triangle BDC

`m\angle BDC+m\angle BCD+m\angle CBD=180^o`

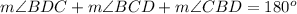
substitute the given values

`37.5^o+37.5^o+m\angle CBD=180^o`

`m\angle CBD=180^o-75^o\\m\angle CBD=105^o`