Question

In ΔUVW, the measure of ∠W=90°, the measure of ∠V=72°, and VW = 6.1 feet. Find the length of UV to the nearest foot.

Answer 1

The length of UV is 19.7 ft.

Solution:

The given
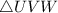`\triangle UVW` is a right triangle because W is 90 degrees. VW is adjacent to V and UV is the hypotenuse. Adjacent any hypotenuse use the cosine function.

Refer the image attached below for the image of the triangle.

`cos\theta=(adj)/(hyp)`

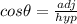
plug in known values

`cos(72\°)=(6.1)/(x)\rightarrow(1)`

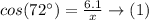
The value of cos(72°) is 0.309

On substituting the above value in (1) we get,

`\Rightarrow0.309=(6.1)/(x)\rightarrow x=(6.1)/(0.309)\rightarrow x=19.7411003236\approx x=19.7`

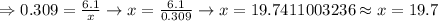
Therefore, the required measure is 19.7 ft.