Question

Let f(x) be a continuous and differentiable function on theinterval, 0<_ x<_ 1, and let g(x)=f(3x). The table below gives the values of f'(x), the derivatives of f(x). What is thevalue of g'(0.1)?

x 0.1 0.2 0.3 0.4 0.5 0.6
f'(x) 1.01 1.041 1.096 1.179 1.298 1.486

Answer 1

Answer:it is b

Explanation:

Answer 2

`g'(0.1)=3.288`

Explanation:

We are given that f(x) be a continuous and differentiable function on interval [0,1]

`g(x)=f(3x)`

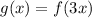
We have to find the value of g'(0.1)

Differentiate w.r.t x

`g'(x)=3f'(3x)`

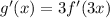
Substitute x=0.1

`g'(0.1)=3f'(3(0.1))=3f'(0.3)`

Substitute the value of f'(0.3) from given table

`g'(0.1)=3(1.096)`

`g'(0.1)=3.288`

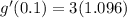
Hence, the value of g'(0.1)=3.288