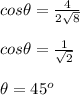Question

The acute angle between intersecting lines that do not cross at right angles is the same as the angle determined by vectors normal to the lines or by the vectors parallel to the lines. Also, note that the vector ai + bj is perpendicular to the line ax + by = c Find the acute angles between the lines: x + √3y = 1 and (1 - √3)x + (1 + √3)y = 8

Answer 1

Acute angle is 45°

Explanation:

Given equation of lines are:

`x+√(3) y=1\\\\√(3) y=-x+1---(1)\\\\(1-√(3) )x+(1+√(3))y=8\\ \\(1+√(3))y=-(1-√(3) )x+8---(2)\\\\`

Line plot of both equations is shown in figure attaches. Red line is for (1) and green is for (2). Angle to be measured is A which is equal to B.

From (1)

`\hat{a}=<1,√(3)>\\`

From(2)

`\hat{b}=<1-√(3),1+√(3)>`

We can find acute angle between two lines as

`cos\theta=(a.b)/(|a||b|)---(3)\\\\a.b=(1)(1-√(3))+(√(3))(1+√(3))\\\\a.b=1-√(3)+√(3)+3\\\\a.b=4\\\\|a|=\sqrt{(1-0)^(2)+(√(3)-0)^(2)} \\\\|a|=√(4) =2\\\\|b|=\sqrt{((1-√(3))-0)^(2)+((1+√(3))-0)^(2)} \\\\|b|=√(8)\\\\`

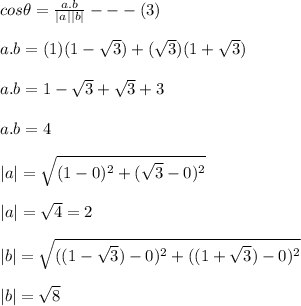
Substituting these values in (3)

`cos\theta=(4)/(2√(8))\\\\cos\theta=(1)/(√(2))\\\\\theta=45^(o)`