Question

The line represented by the equation 4y + 2x = 33.6 shares a solution point with the line represented by the table

below.

x,y
-5, 3.2
-2, 3.8
2, 4.6
4,5
11 ,6.4

The solution for this system is
1) (-14.0,-1.4)
2) (-6.8,5.0)
3) (1.9,4.6)
4) (6.0,5.4)

Answer 1

The solution of this system is

(4). (6.0,5.4)

Explanation:

First we have to find the equation of the line represented in the table; for that we have to find it's slope
`m` and it's y-intercept
`b` and then write it in the following form:

`y=mx+b`

The slope
`m` of the line we get from first two points:

`m=(3.8-3.2)/((-2)-(-5)) =0.2`

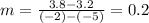
thus we have

`y=0.2x+b`

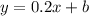
we find
`b` by putting the point
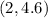`(2,4.6)` into the function:

`4.6=0.2(2)+b`

`b=4.6-0.4=4.2`

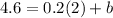
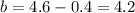
Thus we have

`y=0.2x+4.2`

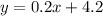
Now we have to find where this line intersects with
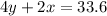`4y+2x=33.6`; to do this we just substitute
`y` with
`y=0.2x+4.2`:

`4(0.2x+4.2)+2x=33.6`

`0.8x+16.8+2x=33.6`

`\boxed{x=6 }`

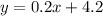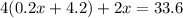
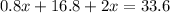
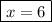
We have the x-coordinate of the intersection.

We find the y-coordinate by substituting
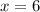`x=6` into
`y=0.2x+4.2`:

`y=0.2(6)+4.2=5.4`

`\boxed{y=5.4}`

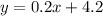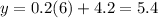
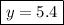
Thus the solution to the system is

`\boxed{(x,y)=(6, 5.4)}`

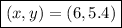
which is option 4.