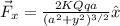Question

A positive point charge Q is located at x=a and a negative point charge −Q is at x=−a. A positive charge q can be placed anywhere on the y-axis. Find an expression for (Fnet)x, the x-component of the net force on q. (Give your answer in terms of Q, q, a, y and constant K.)

Answer 1

`\vec{F}_x = (2KQqa)/((a^2 + y^2)^(3/2)) \^x`

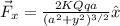
Step-by-step explanation:

The Coulomb's Law gives the force by the charges:

`\vec{F} = K(q_1q_2)/(r^2)\^r`

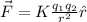
Let us denote the positon of the charge q on the y-axis as 'y'.

The force between 'Q' and'q' is

`F_1 = K(Qq)/(x^2 + y^2)\\F_1_x = F_1\cos(\theta)`

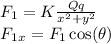
where Θ is the angle between
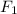`F_1` and x-axis.

`F_1_x = K(Qq)/(x^2 + y^2)((x)/(√(x^2 + y^2))) = (KQqa)/((a^2 + y^2)^(3/2))`

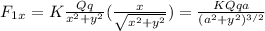
whereas

`F_2_x = K(-Qq)/(a^2 + y^2)(-(a)/(√(a^2 + y^2))) = (KQqa)/((a^2 + y^2)^(3/2))`

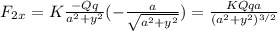
Finally, the x-component of the net force is

`\vec{F}_x = (2KQqa)/((a^2 + y^2)^(3/2)) \^x`