Question

An introduction to statistical methods and data analysis 7th edition:

Suppose a random variable W has a chi-square distribution with df=23. Determine the following probabilites. (Please explain the steps/formula to achieve the answer)
a. P(W > 41.64)
b. P(W > 35.17)
c. P(W <_ 13.09)
d. P(W <_ 12.14)
e. P(W <_ 35.17)
f. P(12.14 < W <_ 35.17)

Answer 1

a) 0.009996

b) 0.050028

c) 0.049989

d) 0.031746

e) 0.949972

f) 0.918226

Explanation:

The Chi Square distribution is the distribution of the sum of squared standard normal deviates .

For this case we have a random variable
`W\sim \chi^2_(df=23)`

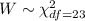
For this case we can use excel in order to find the probabilities.

a. P(W > 41.64) =0.009996

"=1-CHISQ.DIST(41.64,23,TRUE)"

b. P(W > 35.17) =0.050028

"=1-CHISQ.DIST(35.17,23,TRUE)"

c. P(W <_ 13.09) = 0.049989

"=CHISQ.DIST(13.09,23,TRUE)"

d. P(W <_ 12.14) =0.031746

"=CHISQ.DIST(12.14,23,TRUE)"

e. P(W <_ 35.17) =0.949972

=CHISQ.DIST(35.17;23;TRUE)

f. P(12.14 < W <_ 35.17)=0.918226

"=CHISQ.DIST(35.17,23,TRUE)-CHISQ.DIST(12.14,23,TRUE)"