Question

The sun is more massive than the moon, but the sun is farther from the earth. Which one exerts a greater gravitational force on a person standing on the earth? Give your answer by determining the ratio Fsun/Fmoon.

Information:

Earth
mass 5.98 x 10^24 kg
radius (eqt) 6.38 x 10^6 m
Mean distance from the sun 1.50 x 10^11 m

Moon
mass- 7.35 x 10^22 kg
radius (mean) 1.74 x 10^6 m
mean distance from the earth 3.85 x 10^8 m

Sun
Mass- 1.99 X 10^30 kg
Radius 6.96 x 10^8 m

Answer 1

178.4 times

Step-by-step explanation:

We have Newton formula for attraction force between 2 objects with mass and a distance between them:

`F_G = G(M_1M_2)/(R^2)`

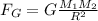
where
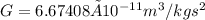`G =6.67408 × 10^(-11) m^3/kgs^2` is the gravitational constant on Earth.
`M_1, M_2` is the masses of the 2 objects. and R is the distance between them.

From here we can calculate the ratio of gravitational force between the moon and the sun

`(F_s)/(F_m) = (G(MM_s)/(R_s^2))/(G(MM_m)/(R_m^2))`

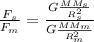
We can divide the top and bottom by G and M

`(F_s)/(F_m)= (M_s)/(R_s^2):(M_m)/(R_m^2)`

`= (M_s)/(R_s^2)(R_m^2)/(M_m)`

`= (M_s)/(M_m)((R_m)/(R_s))^2`

`= (1.99*10^(30))/(7.35*10^(22))((3.85*10^8)/(1.5*10^(11)))^2`

`= 27074830*6.59*10^(-6) = 178.4`

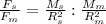
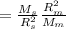
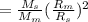
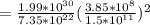
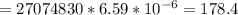
So the gravitational force of the sun is about 178 times greater than that of the moon to an object on Earth