The baker bought 7 gala apples, and 12 granny smiths apples
Solution:
Let "x" be the number of gala apples bought
Let "y" be the number of granny smith apples bought
Cost of 1 gala apple = $ 0.30
Cost of 1 granny smith apple = $ 0.25
A baker buys 19 apples of two different varieties to make pies
Therefore,
number of gala apples bought + number of granny smith apples bought = 19
x + y = 19 --------- eqn 1
The total cost of the apples is $5.10
Therefore, we can frame a equation as:
number of gala apples bought x Cost of 1 gala apple + number of granny smith apples bought x Cost of 1 granny smith apple = 5.10
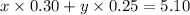
0.3x + 0.25y = 5.1 -------- eqn 2
Let us solve eqn 1 and eqn 2
From eqn 1,
x = 19 - y ---------- eqn 3
Substitute eqn 3 in eqn 2
0.3(19 - y) + 0.25y = 5.1
5.7 - 0.3y + 0.25y = 5.1
5.7 - 0.05y = 5.1
0.05y = 5.7 - 5.1
0.05y = 0.6
y = 12
Substitute y = 12 in eqn 3
x = 19 - 12
x = 7
Thus the baker bought 7 gala apples, and 12 granny smiths apples