Question

Two girls,(masses m1 and m2) are on roller skates and stand at rest, close to each other and face-to-face. Girl 1 pushes squarely against girl 2 and sends her moving backward. Assuming the girls move freely on their skates, write an expression for the speed with which girl 1 moves. ?

Answer 1

`\vec{v}_1 = -\frac{\vec{v}_2m_2}{m_1}`

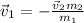
Step-by-step explanation:

The center of mass of the system (two girls) is constant, as the velocity of the center of mass of the system is also constant.

`\vec{v}_(cm) = \frac{m_1\vec{v}_1 + m_2\vec{v}_2}{m_1 + m_2}`

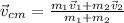
The initial velocity of the system is zero, since both girls are at rest. So the velocity of the total system at any point should be zero as well.

`0 = \frac{m_1\vec{v}_1 + m_2\vec{v}_2}{m_1 + m_2}\\\vec{v}_1 = -\frac{\vec{v}_2m_2}{m_1}`

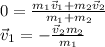
This is true, because there is no friction between the girls and the ground. Otherwise, the velocity of the center of mass wouldn't be constant.