Question

The heights of American men have an approximately bell-shaped distribution with a mean of 70 inches (5' 10") and standard deviation of 3 inches. What is the percentage of American men whose height is between 61 and 79 inches (5' 1" and 6' 7")?

Answer 1

0.9973 is the percentage of American men whose height is between 61 and 79 inches.

Explanation:

We are given the following information in the question:

Mean, μ = 70 inches

Standard Deviation, σ = 3 inches

We are given that the distribution of heights of American men is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

P(height is between 61 and 79 inches)

`P(61 \leq x \leq 79) = P(\displaystyle(61 - 70)/(3) \leq z \leq \displaystyle(79-70)/(3)) = P(-3 \leq z \leq 3)\\\\= P(z \leq 3) - P(z < -3)\\= 0.9987 - 0.0014 = 0.9973= 99.73\%`

`P(61 \leq x \leq 79) = 99.73\%`

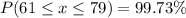
0.9973 is the percentage of American men whose height is between 61 and 79 inches.