Answer:
rm = 38280860.6[m]
Step-by-step explanation:
We can solve this problem by using Newton's universal gravitation law.
In the attached image we can find a schematic of the locations of the Earth and the moon and that the sum of the distances re plus rm will be equal to the distance given as initial data in the problem rt = 3.84 × 108 m
![r_(e) = distance earth to the astronaut [m].\\r_(m) = distance moon to the astronaut [m]\\r_(t) = total distance = 3.84*10^8[m]](https://img.qammunity.org/2021/formulas/physics/middle-school/3dceknyo86d42ntlr42ycpt71nr19hmkt0.png)
Now the key to solving this problem is to establish a point of equalisation of both forces, i.e. the point where the Earth pulls the astronaut with the same force as the moon pulls the astronaut.
Mathematically this equals:
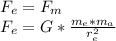
![F_(m) =G*(m_(m)*m_(a) )/(r_(m) ^(2) ) \\where:\\G = gravity constant = 6.67*10^(-11)[(N*m^(2) )/(kg^(2) ) ] \\m_(e)= earth's mass = 5.98*10^(24)[kg]\\ m_(a)= astronaut mass = 100[kg]\\m_(m)= moon's mass = 7.36*10^(22)[kg]](https://img.qammunity.org/2021/formulas/physics/middle-school/c24x4vopq0cehs6todzxxpgrzo3enyi4i3.png)
When we match these equations the masses cancel out as the universal gravitational constant
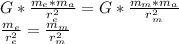
To solve this equation we have to replace the first equation of related with the distances.
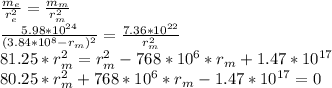
Now, we have a second-degree equation, the only way to solve it is by using the formula of the quadratic equation.
![r_(m1,2)=\frac{-b+- \sqrt{b^(2)-4*a*c } }{2*a}\\ where:\\a=80.25\\b=768*10^(6) \\c = -1.47*10^(17) \\replacing:\\r_(m1,2)=\frac{-768*10^(6)+- \sqrt{(768*10^(6))^(2)-4*80.25*(-1.47*10^(17)) } }{2*80.25}\\\\r_(m1)= 38280860.6[m] \\r_(m2)=-2.97*10^(17) [m]](https://img.qammunity.org/2021/formulas/physics/middle-school/a7qiz0dcm759rgibip37zt1r7zihhiha3y.png)
We work with positive value
rm = 38280860.6[m] = 38280.86[km]