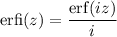Factorize the denominator:
2n² + 3n + 1 = (2n + 1) (n + 1)
Expand the summand into partial fractions:
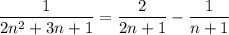
Then the sum is
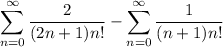
(by the way, you can use \displaystyle to make things like fractions, limits, or sums/integrals render the "right" way)
Recall that for all x,
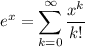
Integrating both sides yields
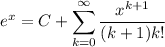
Taking x = 0 leads to C = e⁰ = 1. Move the constant to the left side and divide by x :
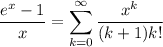
Replacing x with x² in the series for eˣ gives
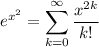
By the fundamental theorem of calculus,
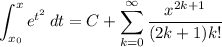
where x₀ is some constant. If we choose x₀ = 0, setting x = 0 elsewhere leads to C = 0.
Putting everything together, the series has a value of
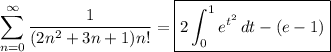
and you could write the integral in terms of the so-called error function,
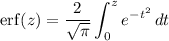
or perhaps more appropriately, the imaginary error function,