Question

In 2002, a gargantuan iceberg broke away from the Ross Ice Sheet in Antarctica. It was approximately a rectangle with dimensions 218 km long, 25.0 km wide, and 250.0 m thick.

A) What is the mass of this iceberg, given that the density of ice is 917 kg/m^3?B) How much heat transfer (in joules) is needed to melt the iceberg?C) How many years would it take sunlight alone to melt ice this thick, if the ice absorbs an average of 109 W/m^2, 12.0 hours per day?

Answer 1

44.46 years

Step-by-step explanation:

Let water fusion heat at atmospheric environment be f = 333550 j/kg

218km = 218000m

25 km = 25000m

a) The iceberg volume is its width times length times thickness:

`V = 25000 * 218000 * 250 = 1.36*10^(12) m^3`

The mass of the iceberg is its density times volume

`m = V*\rho = 1.36*10^(12) * 917 = 1.25*10^(15) kg`

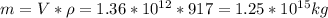
b) The heat energy required to transform the iceberg from solid to liquid form is

`E_h = m*f = 1.25*10^(15)*333550 = 4.167*10^(20)J`

c) Suppose only the upper surface is subjected to sunlight, then we can calculate the sun light area, which is length times width

`A = 218000 * 25000 = 5450000000 m^2`

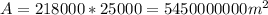
Then the sunlight power, or energy per unit of time that is being transferred to that surface of the iceberg is

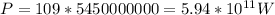`P = 109 * 5450000000 = 5.94*10^(11)W` or J/s

The time it needs (in seconds) to melt:

`t = E_h / P = 4.167*10^(20) / 5.94*10^(11) = 701526032s`

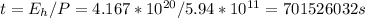
or 701526032 / (60*60) = 194868 hours

As each day only has 12 hours of sunlight, the number of days it'd need is

194868 / 12 = 16239 days or 16239/365.25 = 44.46 years