Answer:
The length of rectangle is 8 unit
The width of rectangle is 48 unit
The Area of rectangle is 384 unit²
Explanation:
Given as :
The perimeter of rectangle = P = 112 unit
The width is 6 times the length
Let The length of rectangle = L unit
Let The width of rectangle = W unit
So, W = 6 × L .........1
Let The Area of rectangle = A unit²
Now, According to question
∵ Perimeter of rectangle = 2 × Length + 2 × Breadth
Or, P = 2 × L + 2 × W
Or, 112 = 2 × L + 2 × 6 × L (from eq 1 )
Or, 112 = 2 × L + 12 × L
Or, 112 = 14 L
∴ L =
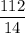
i.e L = 8
So, The length of rectangle = L = 8 unit
Put the value of L into eq 1
∵ W = 6 × L
So, W = 6 × 8
i.e W = 48
So, The width of rectangle = W = 48 unit
Again
∵ The Area of rectangle = (Length × Width) unit²
Or, A = L× W
Or, A = 8 × 48
i.e A = 384 unit²
So, The Area of rectangle = A = 384 unit²
Hence , The length of rectangle is 8 unit
The width of rectangle is 48 unit
The Area of rectangle is 384 unit² Answer