Question

What can we conclude about the triangles on the line shown below?

The triangles are congruent and therefore have the same slope.

The triangles are similar and therefore have the same slope.

The triangles are similar but do not have the same slope.

The triangles are unrelated to one another.

Answer 1

The triangles are similar and therefore have the same slope.

Explanation:

Given:

Two right angled triangles whose hypotenuses lie on the same line.

The line passes through the origin.

The slope of a right angled triangle is the tangent of the interior angle of the triangle that is included between the horizontal side and the hypotenuse.

Let us label the triangles.

From the figure shown below,

Slope of triangle ABC is given as:

Slope ΔABC =
`(BC)/(AB)`

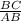
Slope of triangle CDE is given as:

Slope ΔCDE =
`(CD)/(DE)`

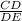
Now consider triangles ABC and CDE.

m ∠ACB = m ∠DCE (Vertically opposite angles are equal)

m ∠ABC = m ∠CDE (Right angles are equal to each other)

Therefore, the two triangles are similar by AA postulate.

Now, for similar triangles, the ratio of their sides are also proportional to each other. So,

`(AB)/(DE)=(BC)/(CD)=(AC)/(CE)\\\\\textrm{Cross multiplying}\\\\(BC)/(AB)=(CD)/(DE)`

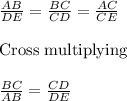
Now, we have, Slope ΔABC =
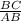`(BC)/(AB)` and Slope ΔCDE =
`(CD)/(DE)`

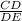
From triangular similarity,
`(BC)/(AB)=(CD)/(DE)`

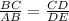
Therefore, Slope ΔABC = Slope ΔCDE

Hence, the triangles are similar and therefore have the same slope.