Question

Two points are located on a rigid wheel that is rotating with an increasing angular velocity about a fixed axis. The axis is perpendicular to the wheel at its center. Point 1 is located on the rim, and point 2 is halfway between the rim and the axis. At any given instant, which point (if either) has the greater angular velocity, angular acceleration, tangential speed, tangential acceleration, centripetal acceleration? Provide a reason for each of your answers.

Answer 1

Same angular velocity

Same angular acceleration

Point 1 has greater tangential speed

Point 1 has greater tangential acceleration

Point 1 has greater centripetal acceleration

Explanation:

Since both points are located on the rigid wheel, their angular velocity and acceleration must be the same for all point located on the wheel.

The tangential quantities, however, would depend on how far they are from the axis of rotation:

`v = \omega R`

`a_T = \alpha R`

`a_c = \omega^2 R`

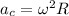
where
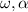`\omega, \alpha` are the angular velocity and acceleration, respectively, which is the same for 2 points. R is the radius of rotation. In this case point 1 has a larger radius since it lies on the rim and point 2 is only half way between.

Therefore, tangential speed, acceleration and centripetal acceleration of point 1 is larger than point 2.