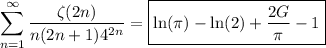Split the summand into partial fractions,
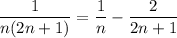
At even integers, the Riemann zeta function has the equivalent form
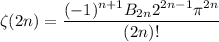
where
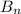 denotes the n-th Bernoulli number.
denotes the n-th Bernoulli number.
Now the sum we want is
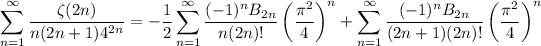
Recall the series expansion for cot(x), valid for 0 < x < π :
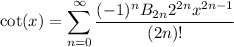
from which we have
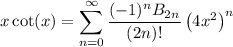
and letting
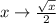 , we get
, we get
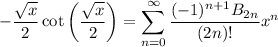
Let
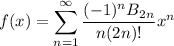
Differentiating both sides gives
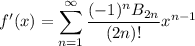
so that
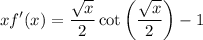
By the fundamental theorem of calculus,
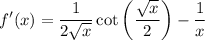
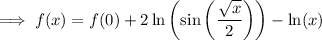
We observe that as x approaches 0, the series vanishes, so we must have
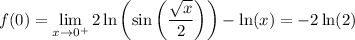
Similarly, let
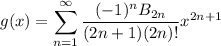
with g(0) = 0, and differentiate to get
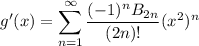
We then have
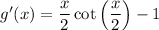
and by the fundamental theorem of calculus,
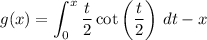
or
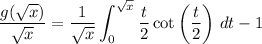
The sum we want is then
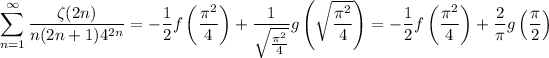
Now we turn our attention to
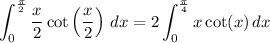
Integrating by parts gives
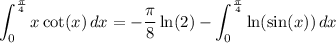
Using the identity from your earlier question [26989784],
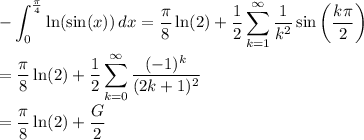
where G is Catalan's constant.
So, it would seem