Question

Giving a test to a group of students, the grades and gender are summarized below. Round your answers to 4 decimal places.

A B C Total
Male 16 13 6 35
Female 2 3 8 13
Total 18 16 14 48
If one student is chosen at random:
1. Find the probability that the student was female AND got a "B".
2. Find the probability that the student was male AND got a "A".
3. Find the probability that the student got a B.

Answer 1

1). 0.1667

2). 0.3333

3). 0.3333

Explanation:

1). Probability that the student was female and got a 'B'

=
`\frac{\text{Number of female students who got B}}{\text{Total number of students}}`

=
`(3)/(48)=(1)/(16)`

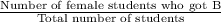
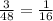
= 0.1667

2). Probability that the student was male and got an 'A'

=
`\frac{\text{Number of male students who got A }}{\text{Total number of students}}`

=
`(16)/(48)`

=
`(1)/(3)`

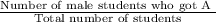
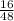
= 0.3333

3). Probability that the student got a B =
`\frac{\text{Number of students who got B}}{\text{Total number of students}}`

=
`(16)/(48)`

=
`(1)/(3)`

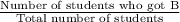
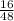
= 0.3333