Answer:
Average value of the function over the interval is 3.
Explanation:
Average value of the function y = 2x³ - 3x² over the interval (-1, 3) will be defined by the area under curve for the given interval divided by width of the interval.
A =
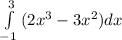
=
![[(2x^(4))/(4)-(3x^(3))/(3)]^(3)_((-1))](https://img.qammunity.org/2021/formulas/mathematics/high-school/gvjt9kcyo1fo97tymucjp61i12pp9n0cz5.png)
=
![[(x^(4))/(2)]^(3)_(-1)-[x^(3)]^(3)_(-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/bj6jp8qf63ozpiz1wdtpx90q5a3qep60m1.png)
=
![[(3^(4)-(-1)^(4) )/(2)]-[3^(3)-(-1)^(3)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/vu8nx95q6h64pf0n568im81ilhmtgg4tiy.png)
=
![[(81-1)/(2)]-[27+1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/2plf8inwds0vz8yecy3qu8ve4quimm3pgp.png)
=
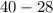
= 12
Width of the interval = 3 - (-1) = 4
Average value =
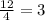
Therefore, average value of the function over the given interval is 3.