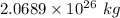Question

The density of a certain planet varies with radial distance as: rho(r)= rho0(1-αr/R0) where R0= 25.12 x 10^6 m is the radius of the planet, rho0= 3800.0 kg/m^3 is its central density, and α = 0.24. What is the total mass of this planet ?

Answer 1

The total mass of this planet is
`2.0689*10^(26)\ kg`

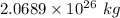
Step-by-step explanation:

Given that,

Radius
`R_(0)=25.12*10^(6)\ m`

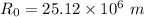
Density
`\rho_(0)=3800.0\ kg/m^3`

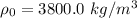
Central density
`\alpha=0.24`

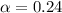
The density of a certain planet varies with radial distance as

`\rho(r)=\rho_(0)(1-(\alpha r)/(R_(0)))`

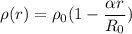
We need to calculate the total mass of this planet

Using formula of density

`\rho=(M)/(V)`

`M=\rho* V`

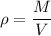
On integrating

`M=\int_(0)^{R_(0)}{\rho(r)*4\pi r^2 dr}`

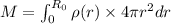
Put the value of
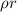`\rho{r}` into the formula

`M=\int_(0)^{R_(0)}{\rho_(0)(1-(\alpha r)/(R_(0)))*4\pi r^2 dr}`

`M=\rho_(0)* 4\pi\int_(0)^{R_(0)}{(r^2-(\alpha r^3)/(R_(0)))dr}`

`M=\rho_(0)* 4\pi*((r^3)/(3)-(\alpha* r^4)/(4* R_(0)))_(0)^{R_(0)}`

`M=4\pi*\rho_(0)* R_(0)^3((4-3\alpha)/(12))`

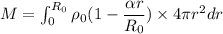
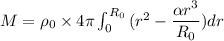
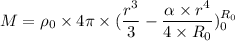
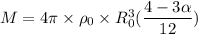
Put the value into the formula

`M=4\pi*3800.0*(25.12*10^(6))^3((4-3*0.24)/(12))`

`M=2.0689*10^(26)\ kg`

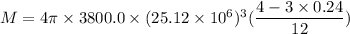
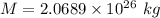
Hence, The total mass of this planet is
`2.0689*10^(26)\ kg`