Question

Un the way to the moon, the Apollo astro-

nauts reach a point where the Moon's gravi-
tational pull is stronger than that of Earth's.
Find the distance of this point from the
center of the Earth. The masses of the
Earth and the Moon are 5.98 x 1024 kg and
7.36 x 1022 kg, respectively, and the distance
from the Earth to the Moon is 3.84 x 108 m.
Answer in units of m.
020 (part 2 of 2) 10.0 points
What would the acceleration of the astro-
naut be due to the Earth's gravity at this
point if the moon was not there? The
value of the universal gravitational constant
is 6.672 x 10-" N.m²/kg?.
Answer in units of m/s?.

Answer 1

To find the distance at which the Moon's gravitational pull is stronger than that of Earth's, set the gravitational forces equal to each other and solve for the distance. The distance from the center of the Earth to this point is approximately 472,397 kilometers.

Step-by-step explanation:

In order to find the distance at which the Moon's gravitational pull is stronger than that of Earth's, we need to set the gravitational forces equal to each other. The gravitational force between two objects is given by the formula:

F = (G * M1 * M2) / r^2

Where F is the force, G is the gravitational constant, M1 and M2 are the masses of the objects, and r is the distance between the centers of the objects.

By setting the gravitational forces equal to each other and solving for r, we can find the distance:

(G * M1 * M2) / r1^2 = (G * M1 * M2) / r2^2

Simplifying the equation, we get:

r1^2 = r2^2 * (M1 / M2)

Substituting the given values, we can calculate the distance of this point from the center of the Earth to be approximately 472,397 kilometers.

Answer 2

Distance = 345719139.4[m]; acceleration = 3.33*10^{19} [m/s^2]

Step-by-step explanation:

We can solve this problem by using Newton's universal gravitation law.

In the attached image we can find a schematic of the locations of the Earth and the moon and that the sum of the distances re plus rm will be equal to the distance given as initial data in the problem rt = 3.84 × 108 m

`r_(e) = distance earth to the astronaut [m].\\r_(m) = distance moon to the astronaut [m]\\r_(t) = total distance = 3.84*10^8[m]`

Now the key to solving this problem is to establish a point of equalisation of both forces, i.e. the point where the Earth pulls the astronaut with the same force as the moon pulls the astronaut.

Mathematically this equals:

`F_(e) = F_(m)\\F_(e) =G*(m_(e) *m_(a))/(r_(e)^(2)  ) \\`

`F_(m) =G*(m_(m)*m_(a)  )/(r_(m) ^(2) ) \\where:\\G = gravity constant = 6.67*10^(-11)[(N*m^(2) )/(kg^(2) ) ] \\m_(e)= earth's mass = 5.98*10^(24)[kg]\\ m_(a)= astronaut mass = 100[kg]\\m_(m)= moon's mass = 7.36*10^(22)[kg]`

When we match these equations the masses cancel out as the universal gravitational constant

`G*(m_(e) *m_(a) )/(r_(e)^(2)  ) = G*(m_(m) *m_(a) )/(r_(m)^(2)  )\\(m_(e) )/(r_(e)^(2)  ) = (m_(m) )/(r_(m)^(2)  )`

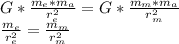
To solve this equation we have to replace the first equation of related with the distances.

`(m_(e) )/(r_(e)^(2)  ) = (m_(m) )/(r_(m)^(2) ) \\(5.98*10^(24) )/((3.84*10^(8)-r_(m)  )^(2)  ) = (7.36*10^(22)  )/(r_(m)^(2) )\\81.25*r_(m)^(2)=r_(m)^(2)-768*10^(6)* r_(m)+1.47*10^(17)  \\80.25*r_(m)^(2)+768*10^(6)* r_(m)-1.47*10^(17) =0`

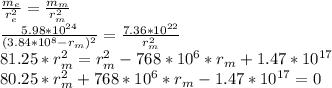
Now, we have a second-degree equation, the only way to solve it is by using the formula of the quadratic equation.

`r_(m1,2)=\frac{-b+- \sqrt{b^(2)-4*a*c }  }{2*a}\\  where:\\a=80.25\\b=768*10^(6) \\c = -1.47*10^(17) \\replacing:\\r_(m1,2)=\frac{-768*10^(6)+- \sqrt{(768*10^(6))^(2)-4*80.25*(-1.47*10^(17)) }  }{2*80.25}\\\\r_(m1)= 38280860.6[m] \\r_(m2)=-2.97*10^(17) [m]`

We work with positive value

rm = 38280860.6[m] = 38280.86[km]

Second part

The distance between the Earth and this point is calculated as follows:

re = 3.84 108 - 38280860.6 = 345719139.4[m]

Now the acceleration can be found as follows:

`a = G*(m_(e) )/(r_(e) ^(2) ) \\a = 6.67*10^(11) *(5.98*10^(24) )/((345.72*10^(6))^(2)  ) \\a=3.33*10^(19) [m/s^2]`