Answer:
12 miles per hour
Explanation:
Let speed of boat in still water be "x"
and speed of current be "c"
So, downstream rate would be "x + c"
And, upstream rate would be "x - c"
Now, given c = 4
We can use the distance formula, D = RT, where
D is distance, R is rate, and T is time
to solve this.
Downstream:
D = RT
92 = (x+4)(t)
Upstream:
D = RT
46 = (x-4)(t)
Both the times are same, we can equate both the times. Lets simplify first:
t = 92/(x+4)
and
t = 46/(x-4)
Equate:
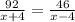
Now, cross multiply and solve for x to get our answer:
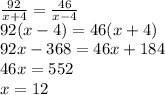
Speed of Boat (in still water) = 12 mph