Answer:
(-5, -6)
Explanation:
The correct question is
The graph of the parent function f(x)=x^3 is translated to from the graph of g(x)=(x+5)^3-6. The point (0,0) on the graph of f(x) corresponds to which point on the graph of g(x)?
see the attached figure to better understand the problem
we have that

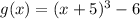
we know that
The turning point in the parent function f(x) is (0,0)
The turning point in the function g(x) is (-5,-6)
so
The translation has the following rule
(0,0) -----> (-5,-6)
(x,y) ----> (x-5,y-6)
The translation is 5 units at left and 6 units down
therefore
The point (0,0) on the graph of f(x) corresponds to (-5,-6) on the graph of g(x)