Answer:
a) Yes
b) Yes
c) Yes
d) No
Explanation:
The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".
The probability mass function for the Binomial distribution is given as:
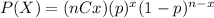
Where (nCx) means combinatory and it's given by this formula:
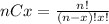
(A) Surveying 100 peoples if they like sudsy soap
Yes, for this case we have a bernoulli experiment on each trial and we have an associated probability if on person satisfy or no the condition. And the value for n is fixed 100, so we can use the binomial model.
(B) Tossing a coin 100 times to see how many heads accur
Yes, for this case we have a bernoulli experiment on each trial and we have an associated probability for head 1/2. And the value for n is fixed 100, so we can use the binomial model.
(C) Drawing a card with replacement from a deck and getting heart
Yes, for this case we have a bernoulli experiment on each trial and we have an associated probability for a heart constant since the experiment is with replacement. And the value for n is fixed 52 the number of cards in a standard deck, so we can use the binomial model.
(D) asking 1000 people which brand of ciggarette they smook
No we can't ensure that we have a bernoulli trial each time so then is not possible. Because we have more than 2 brands probably and on that case the binomial model is not the correct one