Answer:
The given system of equations has solutions below:
1) The solution is (2,3)
2) The solution is (
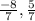 )
)
3) The solution is infinitely many solutions
4) No solution
Explanation:
Given system of equation are


To solve equation by using elimination method
Multiply eqn (2) into 2

Now subtracting (1) and (3)
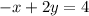
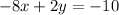
_________________
7x=14
x=
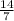

Substitute x=2 in equation (1)
-2+2y=4
2y=4+2

y=3
Therefore the solution is (2,3)
2) Given equation is

4y-4=x
Rewritting as below

To solve equation by using elimination method
multiply (2) into 2

Adding (1) and (3)
-2x+y=3
2x-8y=-8
________
-7y=-5
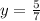
substitute
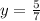 in (1)
in (1)
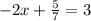

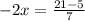
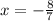
Therefore the solution is (
 )
)
3) Given equation is


equation (1) can be written as
2(3x+y)=10
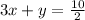
3x+y=5
Therefore equations (1) and (2) are same therefore it has infinitely many solutions
4) Given equation is


multiply equation (1) into 2

To solve equation by using elimination method
subtracting (2) and (3)
-2x-4y=28
-2x-4y=12
_______

therefore it has no solution