Answer:
a) Linear
b) Linear
c) Linear
d) Neither
See explanation below.
Explanation:
a)
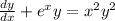
For this case the differential equation have the following general form:
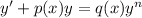
Where
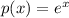 and
and
 and since n>1 we can see that is a linear differential equation.
and since n>1 we can see that is a linear differential equation.
b)
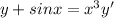
We can rewrite the following equation on this way:
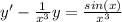
For this case the differential equation have the following general form:
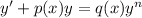
Where
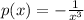 and
and
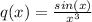 and since n=0 we can see that is a linear differential equation.
and since n=0 we can see that is a linear differential equation.
c)

For this case we can write the differential equation on this way:
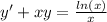
For this case the differential equation have the following general form:
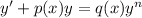
Where
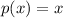 and
and
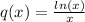 and since n=0 we can see that is a linear differential equation.
and since n=0 we can see that is a linear differential equation.
d)
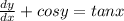
For this case we can't express the differential equation in terms:
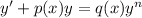
So the is not linear, and since we can separate the variables in order to integrate is not separable. So then the answer for this one is neither.