Question

A cube with a side length of 1008 units is dropped and completely submerged in a cube-shaped container. If the water level in the cube-shaped container rises 252 units. Find the length of a side of the cube-shaped container.

Answer 1

The length of a side of the cube-shaped container is 2,016 units

Explanation:

step 1

Find the volume of a cube with a side length of 1008 units

The volume of a cube is equal to

`V=b^3`

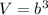
where

b is the length side of the cube

we have

`b=1,008\ units`

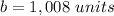
substitute

`V=(1,008)^3\ units^3`

step 2

Find the length side of the cube-shaped container

Let

x-----> the length side of the cube-shaped container in units

we know that

The area of the base of the cube-shaped container multiplied by 252 units must be equal to the volume of the cube with a side length of 1008 units

so

`x^(2) (252)=(1,008)^3`

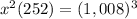
solve for x

`x^(2) =((1,008)^3)/(252)`

`x^2=4,064,256`

`x=√(4,064,256)`

`x=2,016\ units`

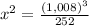
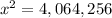
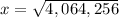
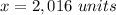
therefore

The length of a side of the cube-shaped container is 2,016 units