Question

Two payment options to rent a car: You can pay $20 a day plus 25¢ a mile (Option A) or pay $10 a day plus 50¢ a mile (Option B). For what amount of daily miles will option A be the cheaper plan?

Answer 1

You must drive more than 40 miles to make option A the cheaper plan

Solution:

Two payment options to rent a car

Let "x" be the number of miles driven in one day

You can pay $20 a day plus 25¢ a mile (Option A)

25 cents is equal to 0.25 dollars

OPTION A : 20 + 0.25x

You pay $10 a day plus 50¢ a mile (Option B)

50 cents equal to 0.50 dollars

Option B: 10 + 0.50x

For what amount of daily miles will option A be the cheaper plan ?

For option A to be cheaper, Option A must be less than option B

Option A < Option B

`20 + 0.25x < 10 + 0.50x`

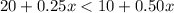
Solve the inequality

Add -0.50x on both sides

`20 +0.25x -0.50x < 10 + 0.50x - 0.50x\\\\20 - 0.25x < 10`

Add - 20 on both sides,

`20 - 0.25x - 20 < 10 - 20\\\\-0.25x < -10`

`\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}`

`0.25x > 10`

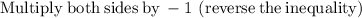
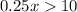
Divide both sides by 0.25

`x > 40`

Thus you must drive more than 40 miles to make option A the cheaper plan