Complete Question:
What is the domain and range of f(x) = |x + 6|?
domain: (negative infinite,infinite); range: f(x) (greater than or equal to) 0
domain: x (less then or equal to)-6; range: (negative infinite,infinite)
domain: x(greater than or equal to)-6 ; range: (negative infinite,infinite)
domain:(negative infinite,infinite) ; range: f(x) (less than or equal to) 0
Answer:
Domain:
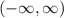 and range:
and range:
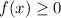
Explanation:
Given:
f(x) = |x + 6|
The vertex of the function is the point (- 6, 0)
The domain is the interval
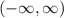 . There are no restrictions on the value x can take. Therefore, the Domain is the set of All Real Numbers or {R}
. There are no restrictions on the value x can take. Therefore, the Domain is the set of All Real Numbers or {R}
The range is the interval
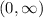 . So,
. So,
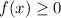 . Because this is a linear transformation the Range is also the set of All Real Numbers or {R}
. Because this is a linear transformation the Range is also the set of All Real Numbers or {R}