The approximate value for t is 5.54
Answer: Option B
Explanation:
The law of cosines generalizes the Pythagorean formula to all triangles. It says that
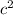 , the square of one side of the triangle, is equal to
, the square of one side of the triangle, is equal to
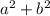 product times the cosine of the opposite angle. When the angle C is right, it becomes the Pythagorean formula.
product times the cosine of the opposite angle. When the angle C is right, it becomes the Pythagorean formula.
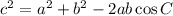
According to the given triangle in figure, the values are
a = 5
b = 4
c = t
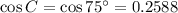
Substituting all the given values in the formula, we get
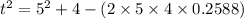
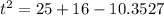
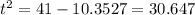
Taking square roots, we get the value for ‘t’ as below,
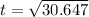
t = 5.536 (approximately 5.54)