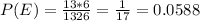Answer:
a) For this case the sample space consists of all the possible pairs of cards, and for this case the order no matter. We need to remember that a standard deck consists of 13 hearts, 13 Clubs, 13 Diamonds and 13 Spades with possible options on each denominaton (A,2,3,4,5,6,7,8,9,10,J,Q,K).
If we want to define the structure for this we can find the size of the sample size using combinatories with the following formula:
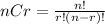
For our case we want to select r =2 cards from n = 52 in total to then we have this:
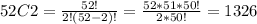 possible pairs.
possible pairs.
b)
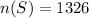
E= draw a pair with the two cars of the same value.
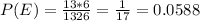
See complete explanation below.
Explanation:
Part a
For this case the sample space consists of all the possible pairs of cards, and for this case the order no matter. We need to remember that a standard deck consists of 13 hearts, 13 Clubs, 13 Diamonds and 13 Spades with possible options on each denominaton (A,2,3,4,5,6,7,8,9,10,J,Q,K).
If we want to define the structure for this we can find the size of the sample size using combinatories with the following formula:
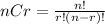
Part b
For our case we want to select r =2 cards from n = 52 in total to then we have this:
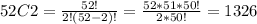 possible pairs.
possible pairs.
So then
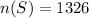 And let define the event:
And let define the event:
E= draw a pair with the two cars of the same value.
From definition of probability:
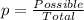
The total outcomes for this case are 1326 and the possible would be 13*6= 78.
The 6 is because for any pair of any card we have 4C2 ways to obtain a pair, because we have a total of 4 cards for each possible outcome, and:
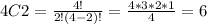
And the 13 is because we have 13 possible cards on the standard deck. So then we can find: