Question

"If two cards are drawn at random without replacement from a standard deck, find the probability that the second card is a face card, given that the first card was a queen.A. 3/13B. 4/17C. 11/51D. 5/17"

Answer 1

C.
`P(F|Q) = (11)/(51)`

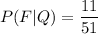
Explanation:

it is to be noted that the question is only asking for the probability of the 2nd card given that the first card was queen
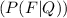`(P(F|Q))`, and not asking for the probability of 1st card to be queen and 2nd card to be faced card
`P(Q\,\text{and}\,F)`

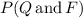
we can represent it in an expression:

`P(Q\,\text{and}\,F) = P(Q)P(F|Q)`

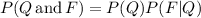
here P(Q) is the first event: Queen

and P(F|Q) is the second event: Faced card, given that the Queen is taken

--------------------------------

we only need to know what is P(F|Q), and that can be found directly found:

let's start with P(Q), what is the probability that the first card is a Queen? Well, there are 4 queens in a standard deck of 52 cards, so the probability should be:

`P(Q) = (4)/(52)`

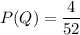
now we have taken our queen, but we haven't put it back in the deck. so the amount of cards in the deck now are 51.

let's calculate P(F|Q),now that one queen is taken out, what is the probability of the next card to be a faced card? Well, in a standard deck there are 12 faced cards, but in our case one queen is already taken out, so there are 11 faced cards in our deck!

`P(F|Q) = (11)/(51)`

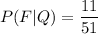
and this our answer!