Answer :
- Length of rectangular court = 31 ft
- Breadth of rectangular court = 10 ft
Explanation:
Given : -
- Perimeter of rectangular court is 82 ft.
- Length = 11 ft longer than twice the width
To Assume : -
- Let length be ( 2x + 11 ) ft ( Because in question it is given that length 11 more than twice it's breadth .
Formula Used : -

Solution : -
We know the given perimeter of rectangle that is 82 ft. So equating it with the perimeter formula :

Step 1 : Substituting the value of length and breadth :
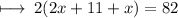
Step 2 : Transposing 2 to right hand side :

Step 3 : By cancelling 82 by 2 we get ;
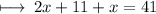
Step 4 : Adding values of left hand side :
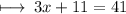
Step 5 : Transposing 11 to right hand side :
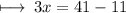
Step 6 : By subtracting 11 from 41 we get :
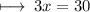
Step 7 : Transposing 3 to right hand side :
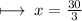
Step 8 : Cancelling 30 by 3 , We get :
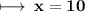
Therefore values,
- Length = 2x + 11 = 2(10) + 11 = 31 ft
Verification : -
We can verify , our answer by substituting values of length and width that we have find above . If th left hand side and right hand side are equal then our answer is correct.
Therefore , our values for length and width are correct / valid .
#Keep Learning