Question

A young couple (who you happen to be very close friends with) purchases a $250,000 house when they are 28 years old. They purchase the house by making a 15% down payment and taking out a 30-year mortgage at an annual interest rate of 7.75% compounded monthly to finance the rest. After 5 years, there is an unforeseen macro-economic event and mortgage rates fall to 3.5%.1 The young couple now has the opportunity to refinance their mortgage by taking out a new 25-year mortgage at 3.5% compounded monthly on their remaining unpaid balance, but they must pay a $2,500 penalty.A strategy outlining an alternative use of the money saved each month by refinancing and the potential value of this strategy to the couple when they retire at 65. Specifically, suppose that the couple spends half of the money that refinancing saves each month as discretionary income aimed at improving their lifestyle and invests the other half in an account where interest is 7.25% compounded monthly.

Answer 1

They will refinance and by using half the amount saved they will end up with a value of $225,017.41 at the end of the mortage in their saving account.

Step-by-step explanation:

House 250,000

downpayment 15% of 250,000 = 37,500

balance 212,500

over 30 years at 7.75% compounded monthly.

monthly payment:

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

PV 212,500

time 360 (30 years x 12 month per year)

rate 0.006458333 (7.75% over 12 month per year)

`212500 / (1-(1+0.00645833)^(-360) )/(0.00645833) = C\\`

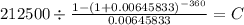
C $ 1,522.376

Balance after 5 year:

PV of the monthly payment at mortgage rate

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 1,522.38

time 300

rate 0.006458333

`1522.376 * (1-(1+0.00645833333333333)^(-300) )/(0.00645833333333333) = PV\\`

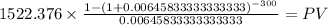
PV $201,551.4404

they will refinance 201,551.44 at 3.5%

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

PV 201,551

time 300

rate 0.002916667

`201551.44 / (1-(1+0.00291667)^(-300) )/(0.00291667) = C\\`

C $ 1,009.014

Difference: 1,522 - 1,009 = 513 dollars

From which they invest half this amount at 7.25% compounded monthly

The future value of this invesmtent will be of:

`C * ((1+r)^(time) -1)/(rate) = FV\\`

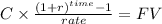
C 256.50

time 300

rate 0.00625

`256.5 * ((1+0.00625)^(300) -1)/(0.00625) = FV\\`

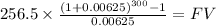
FV $225,017.4136