Question

5) How many solutions does the following system have?

1.5x + 2y = 11
3x + 6y = 22​

Answer 1

The solution is (
`(11)/(1.5)`,0)

The given system of equations have only one solution

(
`(11)/(1.5)`,0)

Explanation:

Given equations are
`1.5x+2y=11\hfill (1)`

and
`3x+6y=22\hfill (2)​`Now to find the number of solutions to the given system:

Multiply the equation (1) into 3 we get

`4.5x+6y=33\hfill (3)`

Subtracting the equations (2) and (3) we get

4.5x+6y=33

3x+6y=22

__________

1.5x=11

`x=(11)/(1.5)`

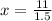
Substitute the value of x in equation (1) we get

`1.5((11)/(1.5))+2y=11`

`11+2y=11`

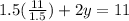
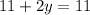
2y=0

Therefore y=0

Therefore the solution is (
`(11)/(1.5)`,0)

The given system of equations have only one solution (
`(11)/(1.5)`,0)