Question

Mercury is a persistent and dispersive environmental contaminant found in many ecosystems around the world. When released as an industrial by-product, it often finds its way into aquatic systems where it can have deleterious effects on various avian and aquatic species. The accompanying data on blood mercury concentration (mu g/g) for adult females near contaminated rivers in a state was read from a graph in an article. 0.21 0.22 0.26 0.30 0.34 0.42 0.55 0.56 1.43 1.70 1.84 2.20 2.25 3.06 3.26 Determine the values of the sample mean and sample median.

Answer 1

The sample mean is
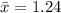`\bar{x}=1.24` and the sample median is 0.56

Explanation:

The sample mean
`\bar{x}` of observations
`x_1,x_2,...,x_n` is given by

`\bar{x}=(\sum x_i)/(n)`

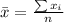
Applying the above definition we get that

The sum of these 15 sample observations is

`\sum x_i = 0.21+\:0.22+\:0.26+\:0.30+\:0.34+\:0.42\:+0.55+\:0.56+\:1.43+\:1.70+\:1.84+\:2.20+\:2.25+\:3.06+\:3.26\\\\\sum x_i =18.6`

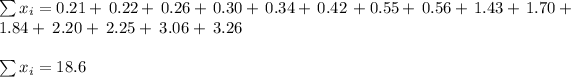
and the sample mean is

`\bar{x}=(18.6)/(15)=1.24`

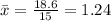
The sample median is obtained by first ordering the n observations from smallest to largest (with any repeated values included so that every sample observation appears in the ordered list). Then,

Sample median = The single middle value if n is odd =
`((n+1)/(2) )^(th)`

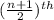
Sample median = The average of the two middle values if n is even = average of
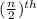`((n)/(2) )^(th)` and
`((n)/(2)+1 )^(th)`

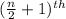
Applying the above definition we get that

The data is already ordered and n = 15 so,

Sample median =
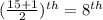`((15+1)/(2) )^(th)=8^(th)` = 0.56