Question

Suppose in the University of Manitoba, 40% of the students live in apartments. If 600 students are randomly selected, then the approximate probability that the number of them living in apartments will be between 200 and 400 is:(A) .9267(B) .9996(C) .9799(D) .9854(E) .987

Answer 1

`P(200\leq X\leq 400)=P((200-240)/(12)\leq (X-\mu)/(\sigma)\leq (400-240)/(12))=P(-3.33\leq Z \leq 13.33)`

`=P(Z<13.33)-P(Z<-3.33)=0.999999-0.000434=0.9996`

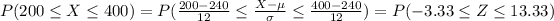
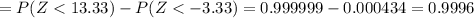
So then the correct answer would be:

B) .9996

Explanation:

The exact way to solve this problem is using the binomial distribution, assuming that our random variable of interest is "number of students living in apartments" represented by X and
`X \sim Bin(n=600, p =0.4)`

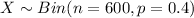
And we want this probability:

And we got:

[tex] P(200 \leq X \leq 400) =0.999675[tex]

But for this case the problem says that we need to approximate, so then we can use the normal approximation to the normal distribution.

We need to check the conditions in order to use the normal approximation.

[tex]np=600*0.4=240\geq 10" src="

`n(1-p)=600*(1-0.4)=360 \geq 10`

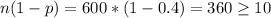
So we see that we satisfy the conditions and then we can apply the approximation.

If we appply the approximation the new mean and standard deviation are:

`E(X)=np=600*0.4=240`

`\sigma=√(np(1-p))=√(600*0.4(1-0.4))=12`

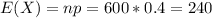
And then
`X \sim N (\mu = 240, \sigma= 12)`

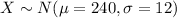
And we are interested on the following probability:

`P(200\leq X\leq 400)=P((200-240)/(12)\leq (X-\mu)/(\sigma)\leq (400-240)/(12))=P(-3.33\leq Z \leq 13.33)`

`=P(Z<13.33)-P(Z<-3.33)=0.999999-0.000434=0.9996`

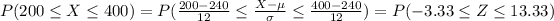
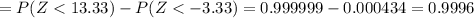
So then the correct answer would be:

B) .9996